Cosmic Rays

CRESCENDO - An on-the-fly Fokker-Planck Solver for Cosmological Simulations

So-called Cosmic Rays (CRs) are protons, electrons and some heavier nuclei moving through galaxies and the entire universe at almost the speed of light. They originate from supernova explosions, jets of active galactic nuclei (AGN) and cosmological shock waves. They provide a number of powerful insights into the plasma physics of the universe.

Radio emission by different clusters in different dynamical states. Image taken from van Weeren (2019).

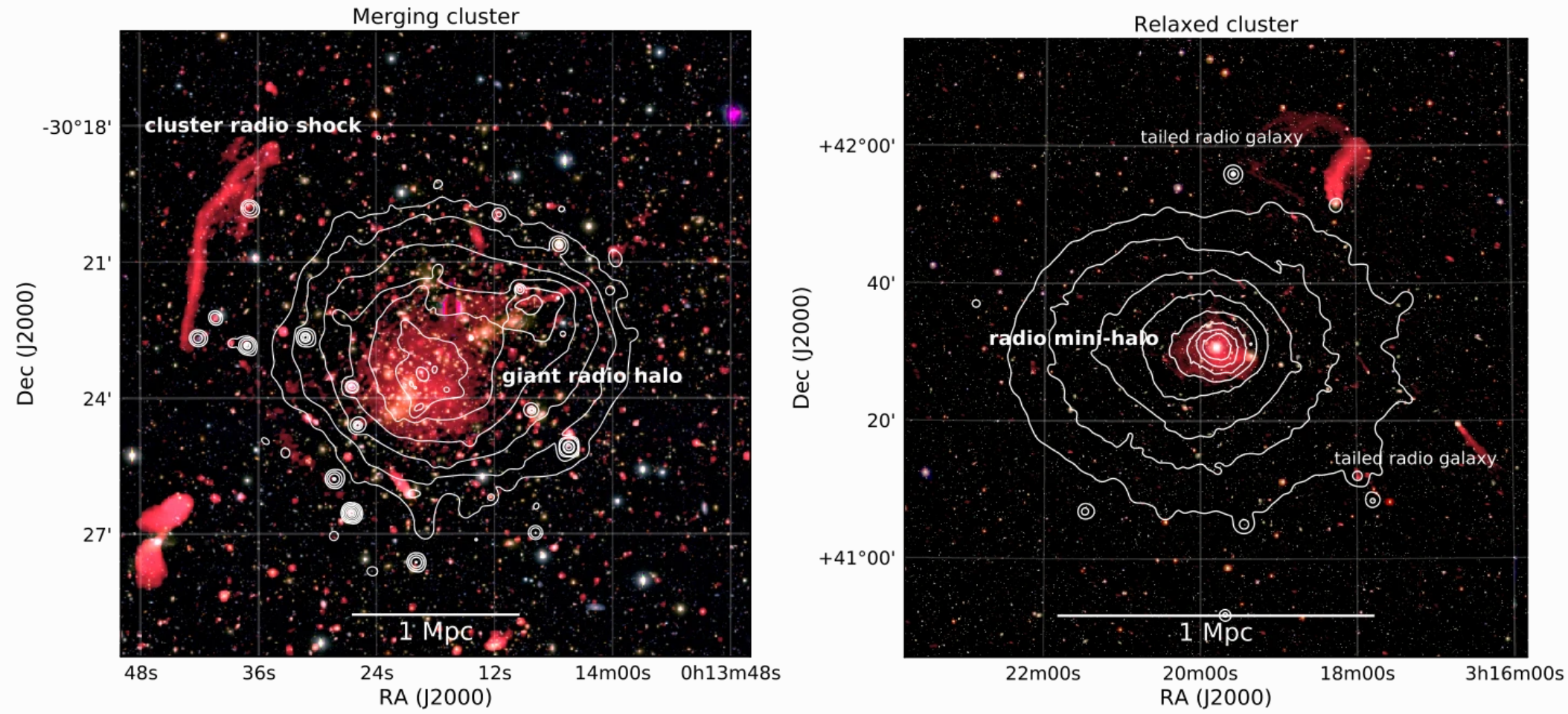
In the case of galaxy clusters CRs are mainly accelerated by structure formation shocks and AGN. As CR electrons move through the magnetized intra-cluster medium (ICM) at relativistic speeds they spiral around magnetic field lines. In this process they loose energy in the form of synchrotron radiation. This synchrotron radiation can be observed as radio relics and radio halos. However the physics behind CR electron acceleration and their re-acceleration by turbulence are not yet fully understood.

Cosmological simulations are a powerful tool to understand the evolution of the universe. Tracing individual electrons or protons in simulations of cosmic structure formation is impossible, as the amount of numerical particles required exceeds the possibility of any current and future super computer.

The central part of my research revolves around implementing an on-the-fly Fokker-Planck solver for cosmological simulations. A Fokker-Planck equation describes how a distribution function evolves in time. In the case of CRs the time evolution of a population of electrons or protons can be described by the Diffusion-Advection Equation

\(\frac{D f(p,\mathbf{x},t)}{Dt} = \nabla \left( \kappa(p) \nabla f(p,\mathbf{x},t) \right)\) \(+ \left( \frac{1}{3} \nabla \cdot \mathbf{u} \right) p \frac{\partial f(p,\mathbf{x},t)}{\partial p}\) \(+ \frac{1}{p^2} \frac{\partial}{\partial p } \left( p^2 \left[ \sum_l b_l f(p,\mathbf{x},t) + D_{\mathrm{pp}} \frac{\partial f(p,\mathbf{x},t)}{\partial p} \right] \right)\) \(- \frac{f(p,\mathbf{x},t)}{t_c(p)}\) \(+ j(\mathbf{x}, p, t)\)

where the terms describe

  1. Total change of the Distribution Function
  2. Diffusion in Physical Space
  3. Adiabatic Changes
  4. Radiative Losses
  5. Turbulent Re-Acceleration
  6. Catastrophic Losses
  7. Sources

My CR model attaches a population of CR electrons and protons to each resolution element of the simulation. I then evolve the distribution function at every timestep of the simulation.

Zoom-in simulation of a galaxy cluster with comparisons to observations.

I mainly focus on studying radio relics and radio halos in galaxy clusters. For this I perform zoom-in simulations of clusters as used in Bonafede et. al. (2011) which include my CR model in different configurations of the aforementioned equation. I am currently working on the related publication where I study the time evoltion of the brightness of the radio halo due to injection of turbulence by shocks and the detailled study of radio relics and how they can be deformed by interaction with the surrounding medium.

Full-Sky projection of CR electron energy density in the energy range E = [5, 500] MeV in the Local Universe Simulations (Böss et. al. (2023c)).

As part of the Localization project we performed a simulation of a $L \sim 740$ Mpc box with constrained initial conditions, which contains my CR model. This allows us to obtain a box around the Milky Way which closely resembles the observed local universe. In this collaboration I lead efforts to study predictions for synchrotron and $\gamma$-ray emission from the local cosmic web.